Staking Methods and Bankroll Management
Workshop
This tutorial was written by Jason and was originally published on Github. It is shared here with his permission.
Good staking systems should be used in combination with betting models. In this article, we’ll go over the basics of staking and analyse some of the more popular staking strategies, outlining their pros and cons.
Why is staking important?
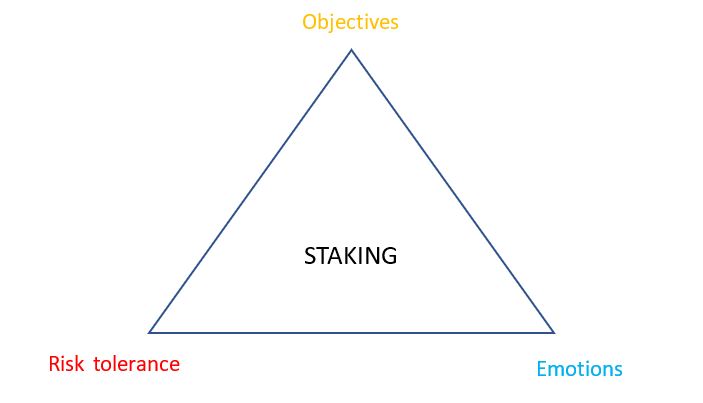
Many bettors with models don’t have sound bankroll management, to their detriment. A good staking system is primarily about balancing risk vs reward:
- If we are too risk inclined and bet aggressively, there is a good chance we will suffer losses
- We want to maximise our returns within our risk constraints
Despite many resources on the web claiming that there is an optimal way to stake, the reality is that there is no one right answer and how you stake will be a personal one which will be affected by:
- Your return objectives
- Your risk tolerance
- Your emotional well-being (we’re not robots)
Your return objectives and risk tolerance are usually the primary considerations when staking and will likely be in conflict with one another and hence will need to be balanced. Generally, chasing higher returns will mean greater levels of risk. Finding the right balance between risk and return that works for you is not an easy task and there will likely be a lot of iterating before getting it right.
The third factor that influences your staking that most people overlook is the impact the size of your bets has on your emotional well-being. Remember that betting should not be stressful and if it is, it probably means that you’re staking too big. Even if your bankroll can theoretically accommodate an increase in your stake sizes, be wary of whether your emotions can.
Common staking systems
Here, we’ll go through some of the more common staking systems. However, rather than just describing each of the staking systems, we’ll attempt to understand the risk/reward profile of each by simulating each staking system 10,000 times based on the following parameters:
- Starting bank of $1,000
- Ruin defined as bank going down to $5 or less (No longer can place a minimum back BSP bet)
- Objective is to quadruple our money
- Assume we have an edge of 5% on all bets
- Each bet is assumed to be between odds of 1.5 and 5, with bets being drawn in this range uniformly
What we’re most interested in seeing is how likely it is that the staking system will succeed on the objective and on average how many bets it takes for success/failure.
Overview of staking methods
| Staking method | Description |
|---|---|
| 1. Fixed Staking | Fixed staking is probably the most simplistic betting system where we bet the same $ amount on every bet no matter what happens to our bankroll in the future Stake = x |
| 2a. Proportional Staking - % of bankroll | Proportional staking defines the bet stake size based on a percentage of your current bank. As your bank increases, the absolute value of your stakes increase and vice versa for when your bank decreases. Stake = Bh h is some chosen fixed % |
| 2b. Proportional Staking - bet to win certain amount | A variant of proportional staking, where for each bet we stake an amount such that if we win, the winning amount is a set % of our bankroll Stake = Bk / (o-1) k is some chosen fixed % o is the odds in decimal form |
3. Martingale Staking |
The Martingale betting system is a progressive betting system whereby after every loss, we stake an amount that (if successful) will recoup all previous consecutive losses and win the original desired amount. After every win, the betting stakes are reset to the initial desired win amount. |
4. Kelly Staking |
Kelly staking or some variant is probably the most popular staking method amongst serious bettors. The Kelly staking formula determines bet size based on the odds of the bet and the assumed edge. Stake = B[(o-1)p - (1-p)] / (o-1) k is some chosen fixed % o is the odds in decimal form |
Pros/Cons
| Staking method | Pros | Cons |
|---|---|---|
| 1. Fixed Staking | - Simple to use |
- Does not account for the size of the current bank - Can take a long time to reach desired objective |
| 2a. Proportional Staking - % of bankroll | - Reduces the risk of ruin by reducing stakes when bank decreases - Maintains the same relative risk-reward profile no matter the size of the bank |
- If you start on a bad run, it can take a long time to recoup your losses |
| 2b. Proportional Staking - bet to win certain amount | - Reduces the risk of ruin by reducing stakes when bank decreases - Compared to proportionally staking a % of bankroll, this method tends to have lower odds slippage |
- If you start on a bad run, it can take a long time to recoup your losses |
5. Martingale Staking |
- Each betting “run” has a high probability of winning - If on a string of good luck, your bank can increase quickly |
- It takes one bad run to wipe out your entire bank .. they do happen! - Highest probability of ruin out of all the staking methods |
6. Kelly Staking |
- Theoretically, it gives the “best” balance of risk vs reward - Varies bet size based on assumed edge |
- Variance is high, bank can be very erratic - Kelly assumes full knowledge of what our edge is. Given we will never know this with certainty, it may lead us to stake too much on low or negative edge bets. |
Simulation results
The following simulation is based on artificial parameters set by Betfair to illustrate the effects of different staking strategies. Of course, gambling is not a reasonable strategy for financial betterment.
| Staking method | Simulation results |
|---|---|
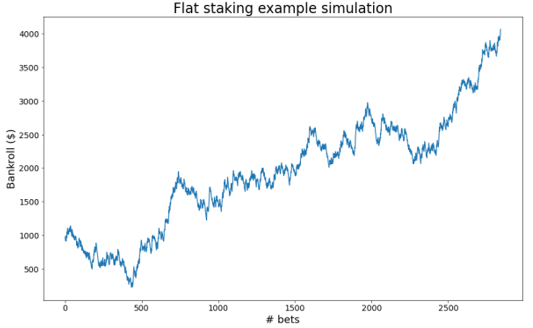
| 1. Fixed Staking | Bet amount: $20 % chance to achieve objective: 89% (2449 bets on average) % chance of ruin: 11% (679 bets on average) Example of simulation success |
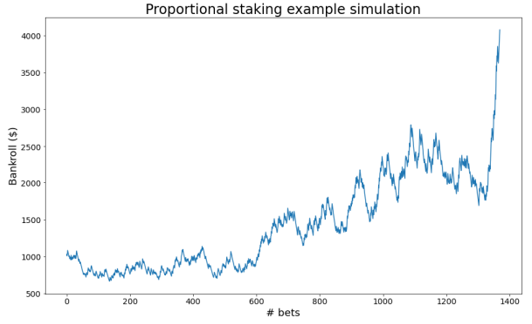
| 2a. Proportional Staking | Bet amount: 2% of bankroll % chance to achieve objective: 97% (1563 bets on average) % chance of ruin: 3% (2893 bets on average) Example of simulation success |
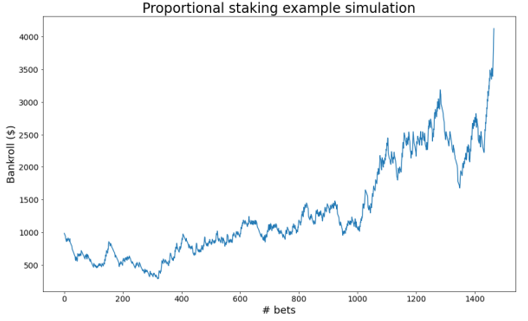
| 2b. Proportional Staking | Bet amount: to win 5% of bankroll % chance to achieve objective: 96% (1074 bets on average) % chance of ruin: 4% (1776 bets on average) Example of simulation success |
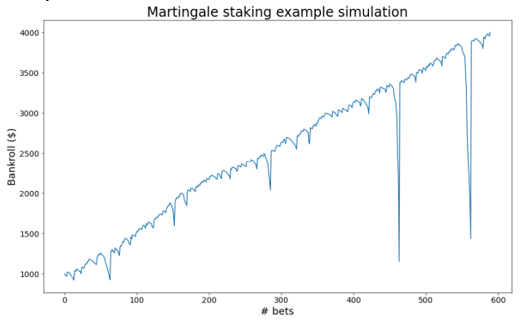
3. Martingale Staking |
Bet amount: to win 3% of bankroll % chance to achieve objective: 46% (408 bets on average) % chance of ruin: 54% (1776 bets on average) Example of simulation success |
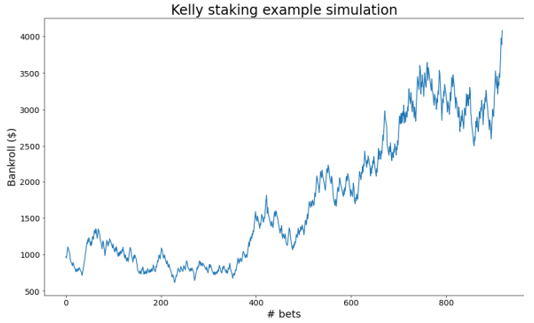
4. Kelly Staking |
Bet amount: Kelly formula % chance to achieve objective: 96% (1071 bets on average) % chance of ruin: 4% (2040 bets on average) Example of simulation success |
Things to watch out for when choosing a staking system
Edge Cliff
A common mistake when deploying a model is to be overly confident in your model’s edge on the market. This is especially problematic when using Kelly staking where edge is a required input into the staking decision.
One thing to be especially wary of when using a model’s theoretical edge in staking decisions is the “edge” cliff where assumed edge and realised edge increase together up to a certain point before dropping markedly. The rationale behind why this happens is because we are unlikely to have perfect information, especially in mature markets where edges beyond a certain amount are unrealistic. Bets that are highlighted from a strategy as having unrealistic edges most likely arise due to the market knowing a key piece of information that we don’t know (e.g. trial information in a race). Hence these bets could actually be our worst performing bets where edge is zero or negative. A Kelly betting system without acknowledging that this can occur can lead to very large decreases in our bank.

Odds Slippage
Before you productionise a model, it’s always good to back-test the model against historic odds if possible. However, be careful about putting too much faith in the Return on Investment (ROI) of your back-test as the prices you’ll actually get will unlikely be the same as the ones in your back-test (odds slippage). This is mainly due to:
- An exchange is dynamic, actions you take will affect the behaviours of other participants on the exchange influencing prices and volumes
- The back-tested ROI will unlikely scale linearly with increased bet sizes, as you stake more you will be forced to take worse prices, especially at larger odds
That is not to say that you shouldn’t back-test your models but you should build in buffers into the back-tests and make assumptions of reasonable but conservative slippage prices. Also, remember to test at small stakes initially, a model may be profitable but unprofitable at larger stakes .. don’t jump to the wrong conclusion!
Complete code
Run the code from your ide by using py <filename>.py, making sure you amend the path to point to your input data.
import random
import numpy as np
def FixedStakesSim(stakeSize, bankroll, ruin, minBet, maxBet, edge, bankObj):
"""
Fixed Stakes Simulation
Parameters
----------
stakeSize : float
stake size for each bet
bankroll : float
starting bankroll
ruin : float
amount where if bankroll drops below, you are ruined
minBet : float
the minimum bet odds which you will bet at
maxBet : float
the maximum bet odds which you will bet at
edge : float
assumed edge for each bet
bankObj : float
your bank objective expressed as a multiple of your starting bank
"""
betRange = maxBet - minBet
dynamicBank = bankroll
# Simulate bets until either objective is achieved or ruined, cap at 50,000 bets
for i in range(50000):
betOdds = round(random.uniform(0,1) * betRange + minBet,2)
winChance = (1 + edge)/betOdds
rand = random.uniform(0,1)
outcome = "Exhausted Bets"
if rand < winChance:
betPnl = stakeSize * (betOdds - 1)
else:
betPnl = -stakeSize
dynamicBank = dynamicBank + betPnl
if dynamicBank > bankObj * bankroll:
outcome = "Objective Achieved"
break
if dynamicBank < ruin:
outcome = "Ruined"
break
if i == 49999:
outcome = "Bets exhausted"
return [outcome, i]
simStore = []
# Simulate 10,000 times
for i in range(10000):
simStore.append(FixedStakesSim(20, 1000, 5, 1.5, 5, 0.05, 4))
probSuccess = len([i[0] for i in simStore if i[0] == 'Objective Achieved']) / len(simStore)
probRuined = len([i[0] for i in simStore if i[0] == 'Ruined']) / len(simStore)
numbetsSuccess = np.median([i[1] for i in simStore if i[0] == 'Objective Achieved'])
numbetsRuined = np.median([i[1] for i in simStore if i[0] == 'Ruined'])
def ProportionalStakesSimA(stakepct, bankroll, ruin, minBet, maxBet, edge, bankObj):
"""
Proportional stakes simulation (staking a % of bankroll)
Parameters
----------
stakepct : float
the % of your dynamic bankroll that you're staking
bankroll : float
starting bankroll
ruin : float
amount where if bankroll drops below, you are ruined
minBet : float
the minimum bet odds which you will bet at
maxBet : float
the maximum bet odds which you will bet at
edge : float
assumed edge for each bet
bankObj : float
your bank objective expressed as a multiple of your starting bank
"""
betRange = maxBet - minBet
dynamicBank = bankroll
for i in range(50000):
stakeSize = max(stakepct * dynamicBank, ruin)
betOdds = round(random.uniform(0,1) * betRange + minBet,2)
winChance = (1 + edge)/betOdds
rand = random.uniform(0,1)
if rand < winChance:
betPnl = stakeSize * (betOdds - 1)
else:
betPnl = -stakeSize
dynamicBank = dynamicBank + betPnl
if dynamicBank > bankObj * bankroll:
outcome = "Objective Achieved"
break
if dynamicBank < ruin:
outcome = "Ruined"
break
if i == 49999:
outcome = "Bets exhausted"
return [outcome, i]
simStore = []
# Simulate 10,000 times
for i in range(10000):
simStore.append(ProportionalStakesSimA(0.02, 1000, 5, 1.5, 5, 0.05, 4))
probSuccess = len([i[0] for i in simStore if i[0] == 'Objective Achieved']) / len(simStore)
probRuined = len([i[0] for i in simStore if i[0] == 'Ruined']) / len(simStore)
numbetsSuccess = np.median([i[1] for i in simStore if i[0] == 'Objective Achieved'])
numbetsRuined = np.median([i[1] for i in simStore if i[0] == 'Ruined'])
def ProportionalStakesSimB(winpct, bankroll, ruin, minBet, maxBet, edge, bankObj):
"""
Proportional stakes simulation (staking to win a certain % of bankroll)
Parameters
----------
winpct : float
the % of your dynamic bankroll that you're staking to win
bankroll : float
starting bankroll
ruin : float
amount where if bankroll drops below, you are ruined
minBet : float
the minimum bet odds which you will bet at
maxBet : float
the maximum bet odds which you will bet at
edge : float
assumed edge for each bet
bankObj : float
your bank objective expressed as a multiple of your starting bank
"""
betRange = maxBet - minBet
dynamicBank = bankroll
for i in range(50000):
betOdds = round(random.uniform(0,1) * betRange + minBet,2)
stakeSize = max((dynamicBank * winpct) / (betOdds - 1), ruin)
winChance = (1 + edge)/betOdds
rand = random.uniform(0,1)
if rand < winChance:
betPnl = stakeSize * (betOdds - 1)
else:
betPnl = -stakeSize
dynamicBank = dynamicBank + betPnl
if dynamicBank > bankObj * bankroll:
outcome = "Objective Achieved"
break
if dynamicBank < ruin:
outcome = "Ruined"
break
if i == 49999:
outcome = "Bets exhausted"
return [outcome, i]
simStore = []
# Simulate 10,000 times
for i in range(10000):
simStore.append(ProportionalStakesSimB(0.05, 1000, 5, 1.3, 5, 0.05, 4))
probSuccess = len([i[0] for i in simStore if i[0] == 'Objective Achieved']) / len(simStore)
probRuined = len([i[0] for i in simStore if i[0] == 'Ruined']) / len(simStore)
numbetsSuccess = np.median([i[1] for i in simStore if i[0] == 'Objective Achieved'])
numbetsRuined = np.median([i[1] for i in simStore if i[0] == 'Ruined'])
def Martingale(winamt, bankroll, ruin, minBet, maxBet, edge, bankObj):
"""
Martingale staking simulation
Parameters
----------
winamt : float
the desired win amount for each betting run
bankroll : float
starting bankroll
ruin : float
amount where if bankroll drops below, you are ruined
minBet : float
the minimum bet odds which you will bet at
maxBet : float
the maximum bet odds which you will bet at
edge : float
assumed edge for each bet
bankObj : float
your bank objective expressed as a multiple of your starting bank
"""
betRange = maxBet - minBet
dynamicBank = bankroll
martingale_win = 1
martingale_progressive_loss = 0
for i in range(50000):
betOdds = round(random.uniform(0,1) * betRange + minBet,2)
stakeSize = max((winamt - martingale_progressive_loss) / (betOdds - 1), ruin)
winChance = (1 + edge)/betOdds
rand = random.uniform(0,1)
outcome = "Exhausted Bets"
if rand < winChance:
betPnl = stakeSize * (betOdds - 1)
martingale_win = 1
martingale_progressive_loss = 0
else:
betPnl = -stakeSize
martingale_win = 0
martingale_progressive_loss = martingale_progressive_loss - stakeSize
dynamicBank = dynamicBank + betPnl
if dynamicBank > bankObj * bankroll:
outcome = "Objective Achieved"
break
if dynamicBank < ruin:
outcome = "Ruined"
break
return [outcome, i]
simStore = []
# Simulate 10,000 times
for i in range(10000):
simStore.append(Martingale(20, 1000, 5, 1.5, 5, 0.05, 4))
probSuccess = len([i[0] for i in simStore if i[0] == 'Objective Achieved']) / len(simStore)
probRuined = len([i[0] for i in simStore if i[0] == 'Ruined']) / len(simStore)
numbetsSuccess = np.median([i[1] for i in simStore if i[0] == 'Objective Achieved'])
numbetsRuined = np.median([i[1] for i in simStore if i[0] == 'Ruined'])
def KellyStake(bankroll, ruin, minBet, maxBet, edge, bankObj, partialKelly):
"""
Kelly staking simulation
Parameters
----------
bankroll : float
starting bankroll
ruin : float
amount where if bankroll drops below, you are ruined
minBet : float
the minimum bet odds which you will bet at
maxBet : float
the maximum bet odds which you will bet at
edge : float
assumed edge for each bet
bankObj : float
your bank objective expressed as a multiple of your starting bank
partialKelly: float
proportion of kelly staking to bet
"""
betRange = maxBet - minBet
dynamicBank = bankroll
for i in range(50000):
betOdds = round(random.uniform(0,1) * betRange + minBet,2)
winChance = (1 + edge)/betOdds
stakeSize = max(((((betOdds - 1) * winChance) - (1-winChance)) / (betOdds - 1)) * dynamicBank * partialKelly,ruin)
rand = random.uniform(0,1)
outcome = "Exhausted Bets"
if rand < winChance:
betPnl = stakeSize * (betOdds - 1)
else:
betPnl = -stakeSize
dynamicBank = dynamicBank + betPnl
if dynamicBank > bankObj * bankroll:
outcome = "Objective Achieved"
break
if dynamicBank < ruin:
outcome = "Ruined"
break
return [outcome, i]
simStore = []
# Simulate 10,000 times
for i in range(10000):
simStore.append(KellyStake(1000, 5, 1.5, 5 ,0.05, 4, 1))
probSuccess = len([i[0] for i in simStore if i[0] == 'Objective Achieved']) / len(simStore)
probRuined = len([i[0] for i in simStore if i[0] == 'Ruined']) / len(simStore)
numbetsSuccess = np.median([i[1] for i in simStore if i[0] == 'Objective Achieved'])
numbetsRuined = np.median([i[1] for i in simStore if i[0] == 'Ruined'])
Disclaimer
Note that whilst models and automated strategies are fun and rewarding to create, we can't promise that your model or betting strategy will be profitable, and we make no representations in relation to the code shared or information on this page. If you're using this code or implementing your own strategies, you do so entirely at your own risk and you are responsible for any losses incurred. Under no circumstances will Betfair be liable for any loss or damage you suffer.